(a)
Since the rate of change of mass is proportional to the difference between energy intake and
energy expenditure, we have
dtdM=k(intake−expenditure)=k(C−30M)■ (b)
To maintain his mass,
dtdMk(C−30M)C=0=0=30M=30(110)=3300■ (c)
dtdM=k(0.8C−30M)dtdM=k(2640−30M)∫88−M1dM=∫30kdt−ln∣88−M∣=30kt+c88−M=Ae−30kt When t=0,
M=110,
88−110=Ae0A=−22
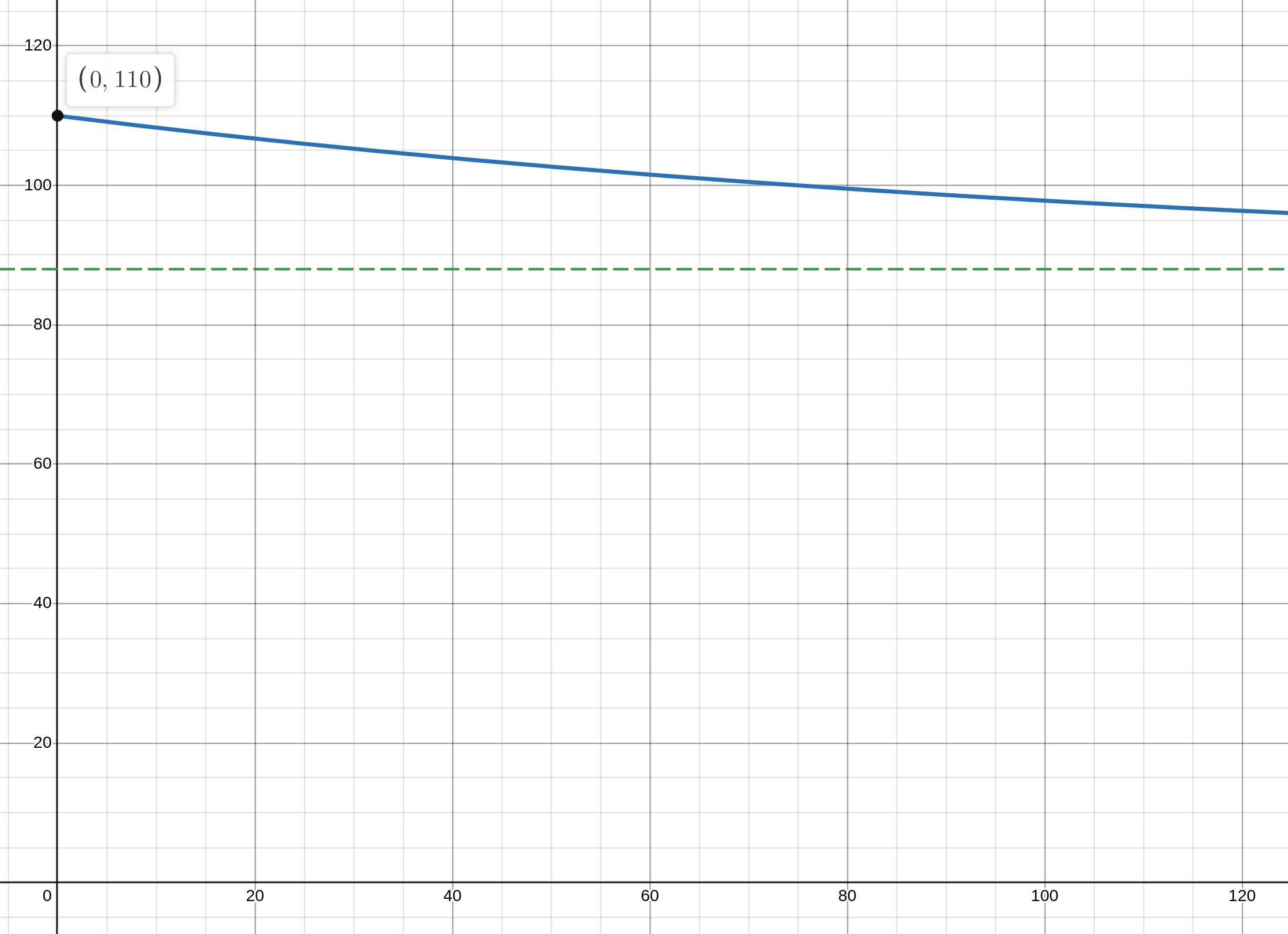
88−M=−22e−30ktM=88+22e−30kt■ (d)
When t=75,
M=100,
100e−2250kk=88+22e−30(75)k=2212=−2250ln116=0.00026939 When his mass falls below 96,
88+22e−30kte−30kt−30kttt<96<228<ln228>−30kln228>125.17
Additional days required=126−75=51 days■ (ei)
Since e−30kt>0
for all real values of t,
M=88+22e−30kt>88 Hence Andrew cannot achieve a mass of 80 kg■
(eii)
For Andrew to achieve a mass of 80 kg,
C−30MCCC<0<30M<30(80)<2400
0<C<2400■