2023 H2 Mathematics Paper Answers

Paper 1

Q1Q2Q3Q4Q5Q6Q7Q8Q9Q10Q11

Short answers to the A Level H2 Math Paper.

Click on the question number to access full solutions.

1 .
y=−10ex+21e.y = - 10 \mathrm{e} x + 21 \mathrm{e}.
2 .
(a)
un=4n3+23n2−46n+29.u_n = 4 n^3 + 23 n^2 - 46 n + 29.
(b)
n≥17.n \geq 17.
3 .
(a)
∣a×b∣=1.\left| \mathbf{a} \times \mathbf{b} \right| = 1.
(b)
θ=135°.\theta = 135 \degree.
4 .
(a)
sin⁡(p+q)x2(p+q)+sin⁡(p−q)x2(p−q)+C.\frac{\sin (p+q)x}{2(p+q)} + \frac{\sin (p-q)x}{2(p-q)} + C.
(b)
xsin⁡nxn+cos⁡nxn2+c.\frac{x \sin nx}{n} + \frac{\cos nx}{n^2} + c.
(c)
k=−2k = -2 or k=0.k = 0.
(d)
π4.\frac{\pi}{4}.
5 .
(a)
ln⁡(n+1n)−ln⁡2. \ln \left( \frac{n+1}{n} \right) - \ln 2.
(b)
−ln⁡2. - \ln 2.
(c)
ln⁡189200. \ln \frac{189}{200}.
6 .
(a)

Show question.

(b)
81π8(π−983).\frac{81 \pi}{8} \left( \pi - \frac{9}{8} \sqrt{3} \right).
7 .
(a)

Asymptotes: y=2y=2 and x=3.x=3.

(b)
Rf=[0,∞). R_f = \left[ 0, \infty \right).
(c)
Rf⊈Df. R_f \not \subseteq D_f.
(d)

Greatest value of a=−2.a = -2.

(e)
f−1(x)=4+3xx−2. f^{-1}(x) = \frac{4+3x}{x-2}.
Df−1=[0,2). D_{f^{-1}} = \left[ 0, 2 \right).
8 .
(a)
z=2e23πi. z = 2 \mathrm{e}^{\frac{2}{3} \pi \mathrm{i}}.
(b)

Smallest positive integer n=2. n = 2.

(c)
w=−4+3i,v=−2w = - 4 + 3 \mathrm{i}, v = - 2
or w=−4+215i,v=−125.\quad w = - 4 + \frac{21}{5} \mathrm{i}, v = - \frac{12}{5}.
9 .
(a)
a=2.a=2.
Coordinates of B=(1,3,6).B = \left( 1, 3, 6 \right).
(bi)
2014. \frac{20}{\sqrt{14}}.
(bii)
θ=63.0°. \theta = 63.0 \degree.
(c)
−3x+4y+z=15.- 3 x + 4 y + z = 15.
10 .
(a)
d⁡ ⁣Md⁡ ⁣t=k(C−30M).\frac{\operatorname{d}\!M}{\operatorname{d}\!t} = k \left( C - 30M \right).
(b)
3300.3300.
(c)
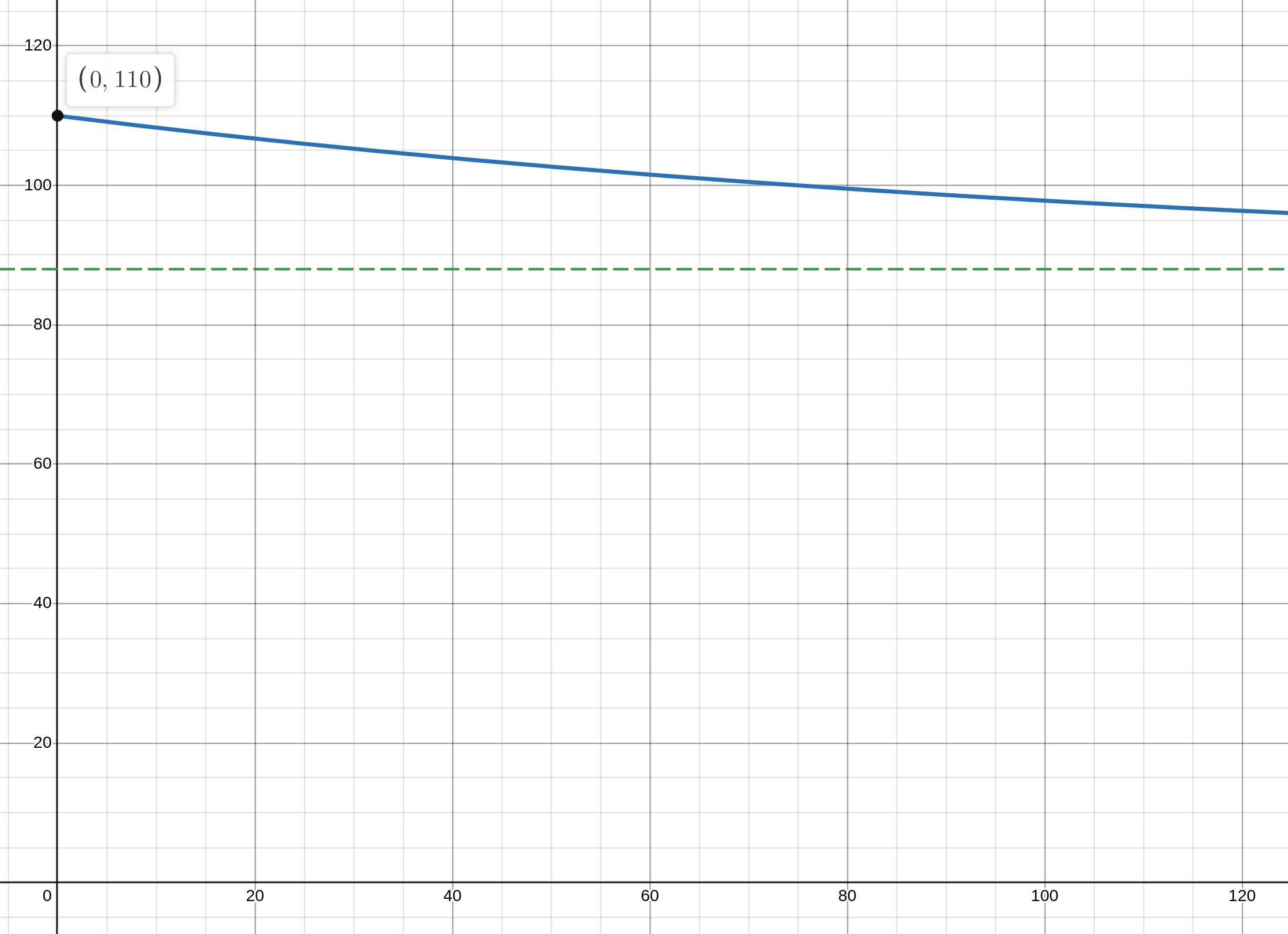
M=88+22e⁡−30kt. M = 88 + 22 \operatorname{e}^{-30kt}.
(d)
51.51.
(ei)
q1-diagram
(eii)
0<C<2400.0 < C < 2400.
11 .
(a)

Smallest a=513.89.a= 513.89.

(b)
400000(1.001)n−400000(1.001)^n - 1000x(1.001n−1).1000x (1.001^n - 1).
(ci)
$1323.63.\$ 1323.63.
(cii)
$76508.52.\$ 76508.52.
(di)
k=287k = 287
y=1321.54.y = 1321.54.
(dii)
$15990.\$15990.